| Переглянути всі підручники | |||||||||||||
| << | < | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | > | >> |
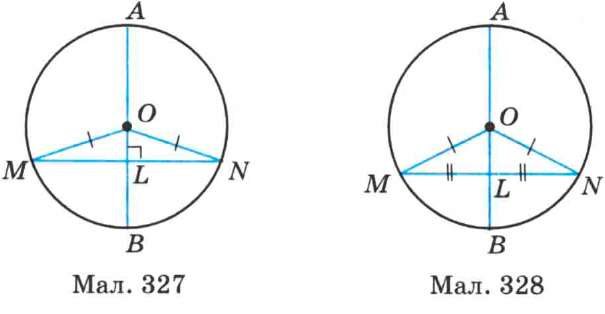
ТеоремаЗ (властивість діаметра кола, перпендикулярного до хорди). Діаметр кола, перпендикулярний до хорди, ділить її навпіл.
Доведення. Нехай діаметр AB кола перпендикулярний до хорди MN, яка відмінна від діаметра (мал. 327). Доведемо, що ML = LN, де L — точка перетину AB і MN.
A MON — рівнобедрений, бо MO = ON (як радіуси). OL — висота рівнобедреного трикутника, проведена до основи. Тому OL є також медіаною. Отже, ML = LN.
Якщо MN є діаметром кола, до твердження теореми очевидне. Теорему доведено.
|
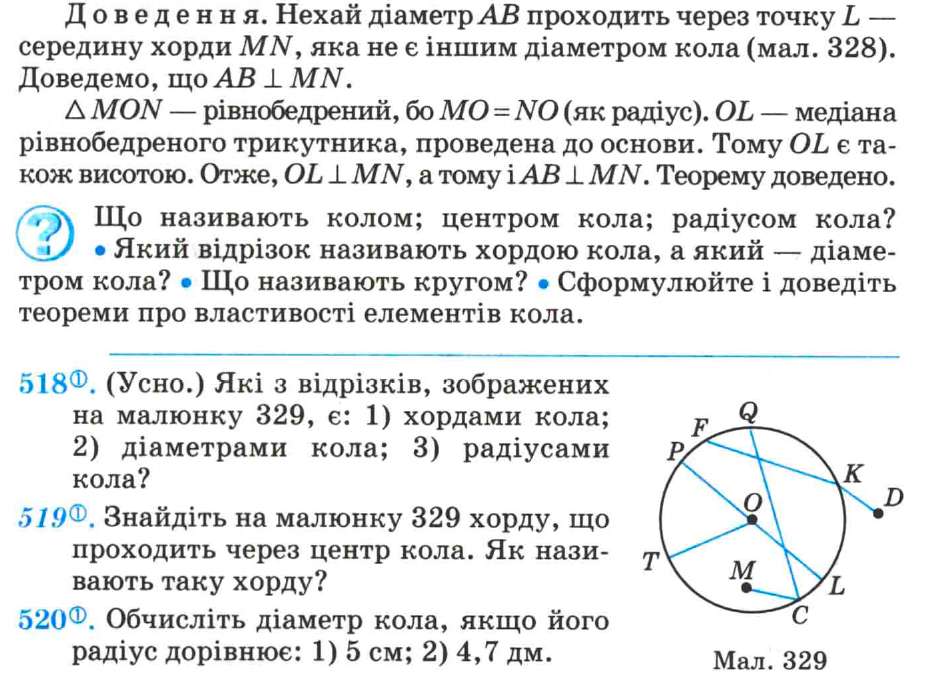
Теорема4 (властивість діаметра кола, що проходить через середину хорди). Діаметр кола, що проходить через середину хорди, яка не є іншим діаметром, перпендикулярний до иієі хорди. |
 |
| Переглянути всі підручники | |||||||||||||
| << | < | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | > | >> |