| Переглянути всі підручники | |||||||||||||
| << | < | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | > | >> |
лінійки без поділок і циркуля. Цими інструментами користувалися ще в Стародавній Греції.
Що можна робити за допомогою двох зазначених інструментів? Лінійка дає змогу провести довільну пряму, побудувати пряму, що проходить через задану точку, і пряму, що проходить через дві задані точки. За допомогою циркуля можна провести коло довільного радіуса, коло з центром у даній точці і радіусом, що дорівнює даному відрізку. В деяких випадках замість кола нам потрібна буде деяка його частина (дуга кола). Зауважимо, що ніяких інших побудов у задачах на побудову виконувати не дозволяється. Наприклад, за допомогою лінійки (навіть із поділками) не дозволяється відкладати відрізок заданої довжини, не можна використовувати косинець для побудови перпендикулярних прямих.
Розв'язати задачу на побудову означає вказати послідовність найпростіших побудов, після виконання яких отримаємо задану фігуру; далі — довести, що побудована фігура має властивості, передбачені умовою, тобто є шуканою фігурою.
Розглянемо найпростіші задачі на побудову.
Побудова відрізка, що дорівнює даному
Задача 1. На даному промені від його початку відкласти відрізок, що дорівнює даному.
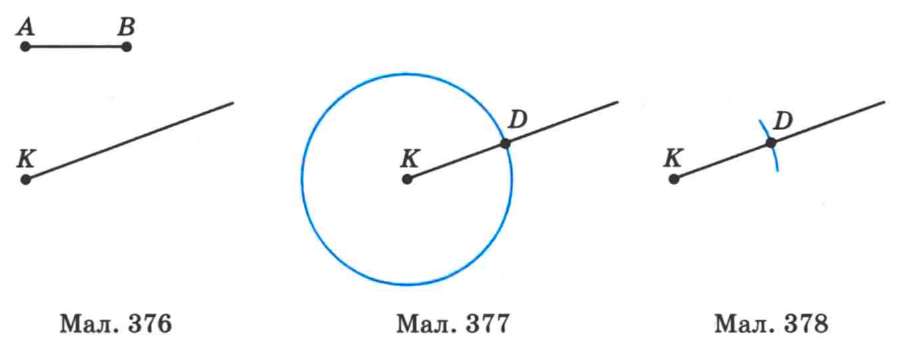
Розв'язання. Зобразимо фігури, задані умовою задачі: відрізок AB та промінь з початком у точці К (мал. 376). Побудуємо циркулем коло з центром у точці К та радіусом AB (мал. 377). Це коло перетне промінь у деякій точці D. Очевидно, що KD = AB. Тому KD — шуканий відрізок.
Зауважимо, що замість кола, можна було провести деяку його частину (дугу), яка б напевне перетинала промінь (мал. 378).
Побудова трикутника за трьома сторонами
Задача 2. Побудувати трикутник із заданими сторонами а,Ь\с.
Розв'язання. Нехай задано три відрізки a, b і с (мал. 379).
| Переглянути всі підручники | |||||||||||||
| << | < | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | > | >> |