| Переглянути всі підручники | |||||||||||||
| << | < | 273 | 274 | 275 | 276 | 277 | 278 | 279 | 280 | 281 | 282 | > | >> |
Урок 38 § 22. ДОТИЧНА ДО КОЛА, її ВЛАСТИВОСТІ
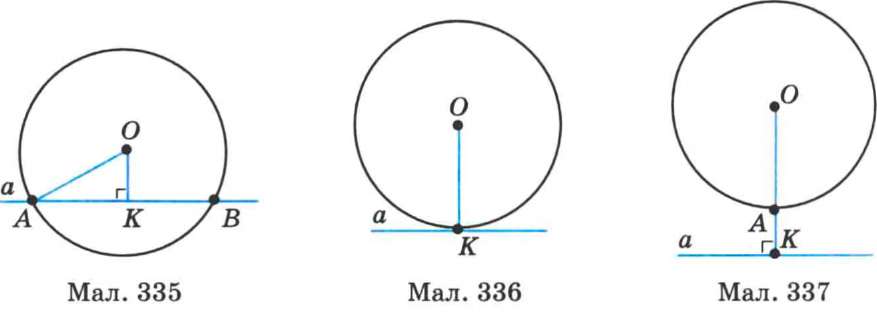
Пряма і коло можуть мати дві спільні точки (мал. 335), одну спільну точку (мал. 336), або не мати спільних точок (мал. 337).
Пряму, яка має дві спільні точки з колом, називають січною. На малюнку 335 OK — відстань від центра кола — точки О — до січної. У прямокутному трикутнику ОКА сторона OK є катетом, а АО — гіпотенузою. Тому OK < OA. Отже, відстань від центра кола до січної менша за радіус.
Якщо пряма і коло не мають спільних точок, то відстань OK більша за радіус кола OA (мал. 337). Відстань від центра кола до прямої, яка не перетинає це коло, більша за радіус.
Теорема 1 (властивість дотичної). Дотична до кола перпендикулярна до радіуса, проведеного в точку дотику.
Дотичною до кола називають пряму, яка має одну спіль

На малюнку 336 пряма а — дотична до кола, точка К — точка дотику.
Якщо пряма і коло не мають спільних точок, то відстань OK більша за радіус кола OA (мал. 337). Відстань від центра кола до прямої, яка не перетинає це коло, більша за радіус.
Теорема 1 (властивість дотичної). Дотична до кола перпендикулярна до радіуса, проведеного в точку дотику.
Доведення. Нехай пряма а дотична до кола з центром у точці О, точка К — точка дотику (мал. 338). Доведемо, що пряма а перпендикулярна до OK.
Припустимо, що пряма а не є перпендикулярною до OK. Проведемо з точки О перпендикуляр ОМ до прямої а. Оскільки у прямої і кола лише одна спільна точка К, то точка М, що належить прямій, лежить поза колом. Тому довжина відрізка ОМ більша за довжину відрізка OA, який є радіусом кола. Оскільки OA =ОК (як радіуси), то ОМ > OK. Але ж, за припущенням, ОМ — катет прямокутного трикутника КОМ, а OK — його гіпотенуза. Прийшли до протиріччя з властивістю прямокутного трикутника (див. § 19, властивість 2).
| Переглянути всі підручники | |||||||||||||
| << | < | 273 | 274 | 275 | 276 | 277 | 278 | 279 | 280 | 281 | 282 | > | >> |