| Переглянути всі підручники | |||||||||||||
| << | < | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | > | >> |
§ 15. МЕДІАНА, БІСЕКТРИСА І ВИСОТА ТРИКУТНИКА. ВЛАСТИВІСТЬ БІСЕКТРИСИ РІВНОБЕДРЕНОГО ТРИКУТНИКА
У кожного трикутника є кілька відрізків, які мають спеціальні назви.
Медіаною трикутника називають відрізок, що сполучає вершину трикутника із серединою протилежної сторони.
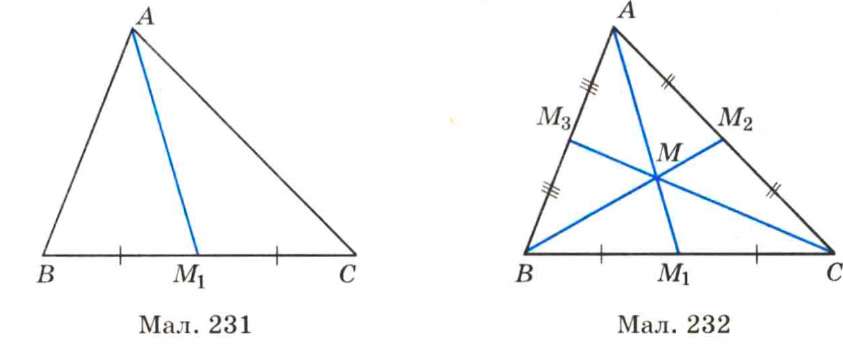
На малюнку 231 відрізок AM t — медіана трикутника ABC. Точку M, називають основою медіани AMj. Будь-який трикутник має три медіани. На малюнку 232 відрізки АМХ, ВМг, СМ:і — медіани трикутника ABC. Медіани трикутника мають цікаву властивість.
У будь-якому трикутнику медіани перетинаються в одній точці (вона називається центроїдом трикутника) і в цій точці поділяються у відношенні 2:1, починаючи від вершини.
На малюнку 232 точка M — центроїд трикутника.

(D
Цю властивість буде доведено у старших класах.
(D
Бісектрисою трикутника називають відрізок бісектриси кута трикутника, що сполучає вершину трикутника з точкою протилежної сторони.

| Переглянути всі підручники | |||||||||||||
| << | < | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | > | >> |